Parallax and Perspective
When projecting to a screen, the intersection may be outside the range of the screen, but that's part of the rendering algorithm, not the projection math.
|
It should be obvious to me, but this is what keeps throwing me off. Purely technically speaking "point" and "vector" (specifically, central vector) ought to be interchangeable, as you're using what has to be defined as a vector space. In a vector space, each point is defined via a central vector, but when you call them "points," my brain shoots to the right and I have to reload.
|
Point and vector are not interchangeable, though many computer applications will use the same structure for both of them, since they store the same data (x, y, and z coordinates). The main problem is that points and vectors have a different set of operations defined for them. If you multiply a constant by a vector, you modify the magnitude of the vector. But what does it mean to multiply a constant with a point? Similarly, you can add vectors (resulting in a new vector), or you can add a vector and a point (resulting in a translated point), but adding two points together has no meaning.
http://www.fimfiction.net/story/36641/My-Little-Exalt
OK, I'm clearly out of my depth running on just memory here. Let me try and explain, instead, things as I would look at them.
I'll be working off the following picture:
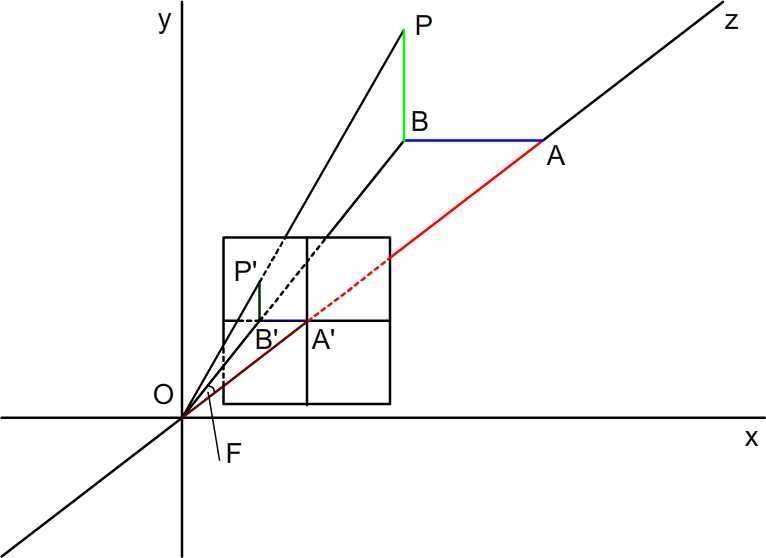
Here, I have the viewing plane aligned to the origin of the coordinate system, such that it's perpendicular to the z axis and in-line with the x and y axes. I've further defined a two-dimensional coordinate system on the plane with an origin where z intersects the plane and with x' and y' coordinate axes (which I forgot to note down, oops!) parallel to the x and y axes of the space. From here on out, I picked a point P defined by its central vector (e.i. defined as P(x,y,z)), and have marked out the physical representations of its coordinates as down on the chart. Red is z, blue is y and green is X. The A, B, A' and B' points I'm using just so that I can call things more easily, and despite having noted the angle between the Z axis and the image of the O->P vector in the xz plane, I probably won't call it by name.
Oh, and before I forget, I've positioned the distance of the viewing plane away from the origin as 1 unit, just to simplify the calculations I'm doing by hand.
Here's what I have in mind: First let's find the image of the O->P vector in the xz plane. That would be OB (noting it as a fixed-length line, lacking a better English term) as B is the image of P on xz. Furthermore, the image of point B onto the z axis is point A. This gives us a triangle OAB, with a right (90 degree) angle at point A. It may not look like that's where it is, but remember - both OA and BA are images of the coordinate axes, which are perpendicular between each other.
By virtue of this being a right angle triangle, I can calculate the tangent of angle BOA, which comes to AB/OA (again, defined just as length values, not as vectors). But because AB = x and OA = z, the tangent of the angle comes up to x/z. Now, because the viewing plane is perpendicular to the x and y axes, and A' and B' are intersection points of OA and OB with the plane, the OA'B' triangle is, in fact, similar to OAB, and because it shares an angle to which we already know the tangent, we can recalculate. Specifically, within triangle OA'B', the tangent of angle B'OA' can be calculated as A'B'/OA'. However, A'B' is actually the x' value of point P by the coordinate system of the viewing plane, and OA' is the distance to the viewing plane, which I defined as 1. This gives us a tan(B'OA') = x'/1 = x'. What's more, because we're looking at the same tangent, that gives us x' = x/z.
I can do an identical process and find out that y' = y/z. I don't want to bore you with it, it's nothing interesting to describe.
This gives me the 3D to 2D transformation of
|x' = x/z
|y' = y/z
For a coordinate system Ox'y' as defined in the viewing plane.
This also tells me one easy thing: A line parallel to the viewing direction will be directed towards the middle of the "screen," crossing it in infinity. The easy answer as to why is that both horizontal and vertical coordinates will decrease, as x and y remain constant, but z (the denominator) increases, causing each subsequent point on the line to converge on the centre as the distance increases. You can also look at it as the angle decreasing, inclining its tangent off centre towards zero, though that's a less interesting way of putting it.
Also, because y' is not affected by the x coordinate of the point, a line parallel to the horizon (where y and z are constant) will transcribe into a line "on screen." Moreover, x' will increase linearly, giving me the function of a line, which I don't feel like bothering to define. It isn't relevant either way.
Basically, that disproves my original claim that lines parallel to the horizon would converge in infinity left and right, necessitating that they be drawn curved, but it does so at the cost of redefining my original model which required refracting through a sphere (and a rather more complicated calculation, involving square roots and variables squared).
Nevertheless, this "flat" model still produces noticeable distortion as you progress away from its centre, only its distortion is angular, rather than curved. I'm not sure which would be more appropriate to describing human eyesight as perceived by the brain, but from the look of things, the flat model is remarkably easier to calculate, which would make it remarkably more suitable for real-time rendering.
*edit*
And again - I graduated from degree a few years ago, and this particular field I studied at the beginning of the course, so it's quite possible I've forgotten a lot, or single-handedly bastardised analysis and geometry. Possibly both.
|
Samuel_Tow is the only poster that makes me want to punch him in the head more often when I'm agreeing with him than when I'm disagreeing with him.
|
|
However, A'B' is actually the x' value of point P by the coordinate system of the viewing plane
|
|
Basically, that disproves my original claim that lines parallel to the horizon would converge in infinity left and right, necessitating that they be drawn curved, but it does so at the cost of redefining my original model which required refracting through a sphere (and a rather more complicated calculation, involving square roots and variables squared).
|
I'm not sure what distortion you're referring to?
http://www.fimfiction.net/story/36641/My-Little-Exalt
Why is that x', then? I neglected to explain, but I define point P's image as the point where OP intersects the viewing plane. However, I can find this image not by tracing it exactly, but by where its image on the zx plane intersects the x' axis, and where its image on the zy plane intersects the y' axis. If I have both, I can extrapolate the the location of the point on the viewing plane by simply adding them up.
If you want, I can prove this geometrically. The whole thing comes down to a pyramid with one edge I didn't draw (because it would have made things REALLY cluttered) that has a base defined by the point, its image on the zx plane, its image on the zy plane and its image on the z axis, and with a peak at the origin O of the 3D coordinate system. This base is perpendicular to the z axis, which is also perpendicular to the viewing plane, which makes the base plane and a viewing plane parallel. As such, the calculations ought to be obvious via trivial proof, combined with a definition I honestly forgot to include.
| And we told you there's no sphere involved... |
 There is no sphere to be had in this model, but this isn't my original model that I used (that one was similar, but more complicated). This one projects directly onto a flat surface via a central translation, whereas the one I originally wanted to go with projected onto a sphere, which then projected onto a flat surface.
There is no sphere to be had in this model, but this isn't my original model that I used (that one was similar, but more complicated). This one projects directly onto a flat surface via a central translation, whereas the one I originally wanted to go with projected onto a sphere, which then projected onto a flat surface.As well, this model uses simple coordinates, whereas the one I originally wanted to use used central coordinates because I didn't want to define a horizon on the view. I could describe that as well, if you want, though I doubt it would be interesting outside of unrelated curiosity, which few have when it comes to mathematics, as far as I've seen. Mathematicians, especially

| I'm not sure what distortion you're referring to? |
|
Samuel_Tow is the only poster that makes me want to punch him in the head more often when I'm agreeing with him than when I'm disagreeing with him.
|
|
This means that the points where OA and OB intersect the viewing plane - A' and B' respectively - form a line between them that lies directly on top of the x' axis of the viewing plane (that square I drew on there).
Why is that x', then? I neglected to explain, but I define point P's image as the point where OP intersects the viewing plane. However, I can find this image not by tracing it exactly, but by where its image on the zx plane intersects the x' axis, and where its image on the zy plane intersects the y' axis. If I have both, I can extrapolate the the location of the point on the viewing plane by simply adding them up. |
|
Perhaps "distortion" is not the right word. What I meant was that as you move away from the centre of the view point and as you increase the field of view, the things you see become increasingly more warped and bizarre, and the actual "normal" portion of the view field shrinks towards the centre. If you'll note when playing Quake 3 Arena with a FOV of, say, 120-150 (I've seen people who do that, for some reason), very little looks like what you'd expect it to look like. It's all out of some bizzarro world that men were not meant to tread.
|
http://www.fimfiction.net/story/36641/My-Little-Exalt
|
But unless I'm reading your previous post wrong (and I'm beginning to think it may have been a typo in the first place), you've claimed that the length of the line segment A'B' is equal to the x-coordinate of the original point P. Which, frankly, can only be possible in two cases: P lies on the z-axis, or O and P are both infinitely far from the plane.
|
The A'B' segment (is that what it's called?
 ) is equal to the x' (x prime) coordinate as plotted on the viewing plane by the viewing plane's separate coordinate system. Essentially, it's the coordinates of the image of the point as counted by the 2D viewing plane's 2D coordinate system.
) is equal to the x' (x prime) coordinate as plotted on the viewing plane by the viewing plane's separate coordinate system. Essentially, it's the coordinates of the image of the point as counted by the 2D viewing plane's 2D coordinate system.This is basically a way for me to calculate a bunch of numbers, then excise the viewing plane out of 3D space entirely disregard anything about this 3D space, and just present the image picture by itself with only the data it holds on its own. Essentially, I want to "print out" the viewing plane on a separate medium as one would save a bitmap or a jpeg.
| Of course changing the FOV will distort the projection. Changing the FOV changes the calculations used for the projection. That's why FOV is only changed when distortions are intended. But given a constant FOV, there's no warping. |
|
Samuel_Tow is the only poster that makes me want to punch him in the head more often when I'm agreeing with him than when I'm disagreeing with him.
|
|
I don't think I'm explaining this well. When I say distortion, I mean that the way the image looks in the corners of the screen is strange, unrealistic and unbelievable, and that cropping just, say, the top-right corner of the screen would look awful. Doing this on a spherical model... Won't, as you can crop out any section and it will look normal within itself.
|
http://www.fimfiction.net/story/36641/My-Little-Exalt
|
I'm sorry, but I simply don't know what you're talking about. Under a perspective projection transformation: points map to points, and straight lines map to straight lines. Parallel lines which are perpendicular to the viewing direction will map to parallel lines along the projection surface, but other parallel lines will map to straight lines which converge to some point, which may or may not be within the screen area.
|
Ah, there we go. Basically, a very high FoV with a flat perspective does this. Centre seems to move farther away (it's actually just smaller) and the bulk of the screen is filled with distorted garbage that's good for little more than seeing if something's moving in it. High FoV with a spherical perspective, by comparison, does this. It's still funky, but every location you look at is consistent within itself and could, conceivably, serve as if you were looking in that direction.
I'll have to do the math on this one, but I'm not terribly convinced a spherical perspective strictly needs a specific viewing direction.
|
Samuel_Tow is the only poster that makes me want to punch him in the head more often when I'm agreeing with him than when I'm disagreeing with him.
|


The sum of a point and a vector is a point translated by a vector (A + v = B; B is A translated by v)
E - P is a vector. c is a scalar. Scalar times a vector is a vector in the same direction with greater magnitude. So, E - P = v1 (a vector), c v1 = v2 (another vector), P + v2 = Pnew (a point)
I know what you're talking about, I just thought the particular subtraction you chose produced a vector in the direction opposite to the one you assumed (which would have honestly did nothing more than make your scalar negative), but since I lacked sufficient knowledge to actually follow the algorithm to the end, it's very likely I just didn't know what you intended to use in the end. Hence why it may not matter.
I'm suddenly reminded why it always took me so long to study for maths exams